Perfectly Spacing Christmas Tree Ornaments

As a follow-up to the problem of how to “Perfectly Light Your Christmas Tree”, the question

“How should ornaments be placed evenly on a Christmas tree?”

naturally arose, and my answer to this question is provided below in a sequence of steps.

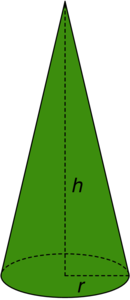
Disclaimer: 

The solution that I obtained to this problem does not lend itself to providing a “real-time” calculator like the Christmas Tree Lights Spacing Calculator. A computer program was written, however, to obtain the solution and generate animations that illustrate the solution.

Step 0

The first step in solving the problem, like the solution to spacing the lights on the tree, is to model the Christmas tree as a right-circular cone. Since our Christmas tree has a radius r = 1¾ feet (i.e., a diameter of 3½ feet) at its base and a height h = 8 feet, these dimensions are used as defaults in my calculations.

Step 1

Next, I considered the similar problem of how to evenly place points inside a circle (of radius r). The Lord has placed the Golden ratio, Golden spiral, Golden angle, and Fibonacci numbers throughout His creation, and the sunflower is an example of His fingerprint on His creation. The florets of the sunflower are arranged in Golden spiral patterns, and the number of clockwise and counter-clockwise spirals are Fibonacci numbers. The animation below demonstrates this design.

Given \(N\) points to “equally” space inside a circle of radius r, I used Vogel's method to produce the Fermat's Golden spiral pattern inside the circle. The image below shows how to space \(N=200\) points in a circle, and this serves as the basis for spacing \(N=200\) ornaments on a tree (excluding the center of the circle which will be reserved for a “tree topper”).

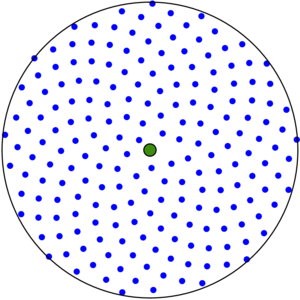
These \(N\) spiral points \((x_i,y_i)\) are parameterized by \[ \begin{array}{rcl} x_i & = & \rho_i\cos(i\varphi)\\ y_i & = & \rho_i\sin(i\varphi) \end{array}\] where \(\displaystyle\varphi=\pi(3-\sqrt{5})\) is the Golden angle (in radians), \(\rho_\text{min}\) is the minimum radius where the points begin (e.g., \(\rho_\text{min}=r/100\)), and \[ \rho_i=\rho_\text{min} + (r-\rho_\text{min})\sqrt{\frac{i}{N-1}} \] with \(0\leq i\leq N-1\).

Step 2

Once the points in the circle have been “equally” spaced using the sunflower model, the points (ornaments) are then lifted in order to place them on the cone (tree). This can be interpreted as lifting the center of the circle to a height h above the circle and thus forming the cone (tree).

Specifically, \[ z_i = h\left(1-\frac{\rho_i}{r}\right), \] and the red points are the lifted ornaments whereas the blue points are the original points in the base circle.

Step 3

Now that the \(N\) ornaments have been lifted to the tree, I then made some adjustments to ensure even spacing. The first step is to insert an additional placeholder ornament at the top of the cone (to reserve space for the tree-topper). In order to keep ornaments from accumulating at the bottom of the cone, I also inserted N+1 additional placeholder ornaments onto a vertically reflected cone (resulting in a total of N ornaments and N+2 placeholder ornaments).

In order to recursively adjust each of the \(N\) ornaments, they are interpreted as electrons on a cone. Since like charges repel, the electrons will try to spread away from one another as much as possible. However, each electron cannot spread too far away because, otherwise, it will begin to approach another electron. The dispersion process nudges each electron in the direction of the net Coulomb force acting on it. The Coulomb force acting on the \(i^{\text{th}}\) ornament due to the \(j^{\text{th}}\) ornament \((j\neq i)\) is the force \[ \vec{f}_{\!i,j} = \frac{\vec{\Delta}_{i,j}}{\left\|\vec{\Delta}_{i,j}\right\|^3} \] where \[ \vec{\Delta}_{i,j} = \big\langle x_i-x_j,y_i-y_j,z_i-z_j\big\rangle, \] and thus the (total) net force acting on the \(i^{\text{th}}\) ornament by the other 2N+1 other ornaments is \[ \vec{F}_i = \sum_{\underset{\scriptstyle j\neq i}{j=1}}^{2N+2} \vec{f}_{\!i,j} \]

Each of the \(N\) ornaments are moved in the direction (and by an amount proportional to the magnitude) of \(\vec{F}_i\) (\(1\leq i\leq N\)), and then each ornament is projected back onto the cone. The animation below illustrates several iterations of this dispersion process (watch carefully).

Step 4

Once the dispersion reaches equilibrium, the position of the ornaments is complete. The last animation shows the position of all of the ornaments (by rotating the tree).